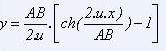Chaînette ou Funiculaire
Je ne sais plus bien si j'ai découvert la chaînette en
MathElem ou en MathSup, car il fallait pour cela connaître les
fonctions hyperboliques (qui figuraient alors au programme de MathElem)
et les équations différentielles (qui devaient
être, elles, au programme de MathSup). Plus tard, en école
d'ingénieurs, et plus précisément en cours de
résistance des matériaux, j'ai eu à étudier
les structures funiculaires (c'est-à-dire faites de cordages) en
détail : je ne savais pas alors que j'aurais un jour à
enseigner cela à mon tour à des étudiants de la
faculté des sciences à Rennes;
Une chaînette ou funiculaire est censée représenter
la courbe que prend un objet filiforme pesant (c'est-à-dire de
dimensions transversales négligeables par rapport à sa
longueur), suspendu entre ses deux extrémités. En
résistance des matériaux, on étudie toutes sortes
de chaînettes : à densité de charge non uniforme,
avec des mases accrochées en certains points, avec les
extrémités situées à des hauteurs
différentes, etc. Nous ne nous intéresserons ici qu'au
cas le plus simple, celui où :
- la densité de charge est uniforme
- les deux extrémités sont au même niveau horizontal
Soit donc une chaînette de longueur l et de masse totale m
uniformément répartie ; on la suspend par ses deux
extrémités A et A' situées au même niveau
horizontal (cf. figure ci-dessous) ; la courbe étant
évidemment plane et symétrique verticalement, on prend
pour axes de coordonnées : Oy son axe de symétrie
verticale, Oy l'horizontale la plus basse en contact avec la courbe :
:
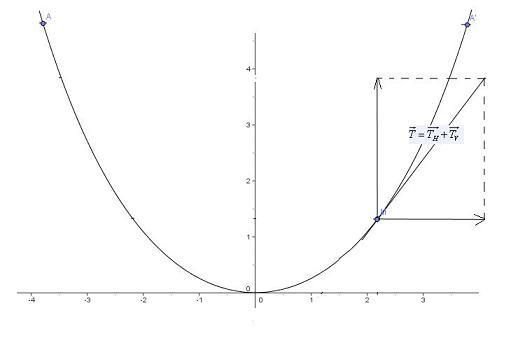
On ne s'intéresse qu'à la moitié OA'.
En un point
M de la courbe, l'effort de traction total se décompose en ses
composantes horizontale et verticale :
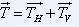
Or, l'effort de traction du tronçon MA' sur le reste
de la chaînette est tangent à la courbe (une chaîne
ou corde ne peut transmettre d'efforts perpendiculaires). Donc
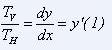
Or,
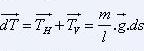
Donc
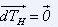ce
qui signifie que la composante horizontale de la traction est constante
tout le long de la chaînette,et
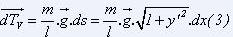
De (1) et (3), on déduit que
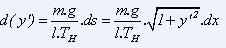
donc
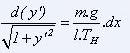
qui permet, par intégration de connaître y' :
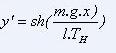
et, en tenant compte des conditions aux limites, par une nouvelle
intégration, de connaître y :
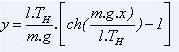
Pour obtenir TH, on écrit qu'en A', on a y' = TV/TH, donc :
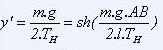
En posant :
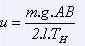
on déduit que :
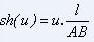
et on détermine u tel
que :
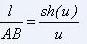
En résumé, une fois connu u racine de l'équation
implicite précédente, on calcule la traction horizontale
par la formule :
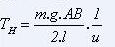
et on trace la courbe à l'aide de l'équation suivante :
