Energie stockée dans un
condensateur
Lorsqu’on empile des briques de masse m1, m2, m3, m4, etc. les unes
sur les autres, chaque nouvelle brique augmente la hauteur H du tas de
brique et nécessite plus d’énergie pour être montée
jusqu’au sommet du tas. Cette énergie supplémentaire est
égale à Wi = H.mi (formule dans laquelle H varie avec mi).
De la même façon, lorsqu’on empile des charges q1, q2,
q3, q4, etc. dans un condensateur, chaque nouvelle charge augmente la tension
U aux bornes du condensateur et nécessite une quantité d’énergie
Wi = U.qi (formule dans laquelle U varie avec qi).
Or la tension U est égale à tout moment au rapport q/C.
Mathématiquement on écrit que la variation de d’énergie
dW est égale à (1/C).q.dq
L’intégrale de dW de l’origine de la charge (q=0) à la
fin de la charge (q=Q) vaut donc (1/C).(1/2).Q2 = (C.U)/2.
 Si on veut
éviter le calcul intégral, on peut constater que l’énergie
accumulée est indépendante de la façon dont la charge
a lieu. On peut donc supposer qu’on l’effectue de façon linéaire,
c’est-à-dire en faisant varier U en fonction de q comme indiqué
sur le graphique ci-dessous. On voit que les dernières charges correspondent
à une énergie égale à q.Umax alors que les
premières s’accumulent sous une énergie pratiquement nulle
(tension voisine de zéro). Il est donc légitime de supposer
que c’est équivalent énergétiquement de charger qmax
à mi-tension, d’où le coefficient ½.
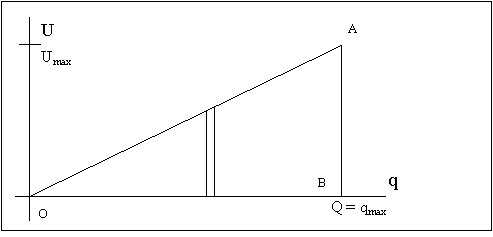
Si on veut
éviter le calcul intégral, on peut constater que l’énergie
accumulée est indépendante de la façon dont la charge
a lieu. On peut donc supposer qu’on l’effectue de façon linéaire,
c’est-à-dire en faisant varier U en fonction de q comme indiqué
sur le graphique ci-dessous. On voit que les dernières charges correspondent
à une énergie égale à q.Umax alors que les
premières s’accumulent sous une énergie pratiquement nulle
(tension voisine de zéro). Il est donc légitime de supposer
que c’est équivalent énergétiquement de charger qmax
à mi-tension, d’où le coefficient ½.
On peut aussi remarquer que chaque charge qi supplémentaire correspond
à à une " tranche " du triangle OAB. Ajouter toutes les "
tranches " revient à calculer l’aire du triangle OAB, d’où
le coefficient ½ à nouveau.
 Si on veut
éviter le calcul intégral, on peut constater que l’énergie
accumulée est indépendante de la façon dont la charge
a lieu. On peut donc supposer qu’on l’effectue de façon linéaire,
c’est-à-dire en faisant varier U en fonction de q comme indiqué
sur le graphique ci-dessous. On voit que les dernières charges correspondent
à une énergie égale à q.Umax alors que les
premières s’accumulent sous une énergie pratiquement nulle
(tension voisine de zéro). Il est donc légitime de supposer
que c’est équivalent énergétiquement de charger qmax
à mi-tension, d’où le coefficient ½.
Si on veut
éviter le calcul intégral, on peut constater que l’énergie
accumulée est indépendante de la façon dont la charge
a lieu. On peut donc supposer qu’on l’effectue de façon linéaire,
c’est-à-dire en faisant varier U en fonction de q comme indiqué
sur le graphique ci-dessous. On voit que les dernières charges correspondent
à une énergie égale à q.Umax alors que les
premières s’accumulent sous une énergie pratiquement nulle
(tension voisine de zéro). Il est donc légitime de supposer
que c’est équivalent énergétiquement de charger qmax
à mi-tension, d’où le coefficient ½.