ELECTROMAGNETISME ET NOMBRES COMPLEXES, TROISIEME PARTIE
(cette troisième partie est consacrée aux impédances et à leur représentation dans le plan)
Dans la première partie, nous avons vu dans quelles conditions on pouvait associer à des grandeurs scalaires réelles, telles que tensions et intensités, des grandeurs complexes, permettant de simplifier les calculs en éliminant formellement « la variable temps », et donc en ramenant des « calculs en courant alternatif » à des « calculs en courant continu ». Dans la seconde partie, nous avons examiné comment transposer les mêmes méthodes aux grandeurs vectorielles.
Dans cette troisième partie nous abordons un aspect assez
différent de l’utilisation des nombres complexes : il s’agit des
impédances et de leur représentation graphique dans le plan complexe. Plus
précisément, nous nous intéresserons aux combinaisons de selfs et de ![]() condensateurs tels que les utilisent les radio-amateurs
lorsqu’ils s’intéressent aux transformations et aux adaptations d’impédance, en
particulier entre lignes et antennes. La représentation graphique des
impédances permet alors de « visualiser les transformations » et de
mieux comprendre ce qu’on fait, éventuellement de modifier les combinaisons de
selfs et de condensateurs pour couvrir d’autres gammes d’impédances. Nous
traiterons le sujet à partir d’exemples.
condensateurs tels que les utilisent les radio-amateurs
lorsqu’ils s’intéressent aux transformations et aux adaptations d’impédance, en
particulier entre lignes et antennes. La représentation graphique des
impédances permet alors de « visualiser les transformations » et de
mieux comprendre ce qu’on fait, éventuellement de modifier les combinaisons de
selfs et de condensateurs pour couvrir d’autres gammes d’impédances. Nous
traiterons le sujet à partir d’exemples.
Premier exemple : représentation graphique d’une impédance et d’impédances en série
|
y’ |
A
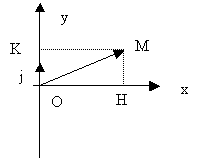
chaque impédance complexe de la forme Z=R+j.Y avec (R et Y réels), on associe
le vecteur si si
si
si
La
mise en série de deux impédances correspondra simplement à l’addition de 2
vecteurs (les parties réelles s’ajoutent, les parties imaginaires s’ajoutent. |
Second exemple : représentation graphique de la mise
en parallèle d’une résistance pure et d’une réactance pure
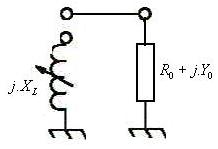
Supposons qu’on dispose d’une impédance comportant une
partie résistive![]() et une partie réactive
et une partie réactive ![]() (par exemple une
antenne non résonante). L’image de
(par exemple une
antenne non résonante). L’image de![]() dans le plan complexe est le point M0 . Dans le
cadre de la construction d’un circuit d’accord, on installe en parallèle une
self variable d’impédance
dans le plan complexe est le point M0 . Dans le
cadre de la construction d’un circuit d’accord, on installe en parallèle une
self variable d’impédance ![]() variable. La question
est de savoir comment varie l’impédance résultante
variable. La question
est de savoir comment varie l’impédance résultante![]() en fonction des variations de la self. Plus précisément, la
question est de savoir comment se déplace dans le plan complexe le point M,
correspondant à
en fonction des variations de la self. Plus précisément, la
question est de savoir comment se déplace dans le plan complexe le point M,
correspondant à ![]() . Calculons
. Calculons![]() par les formules habituelles :
par les formules habituelles :
![]() qu’on peut
aussi écrire
qu’on peut
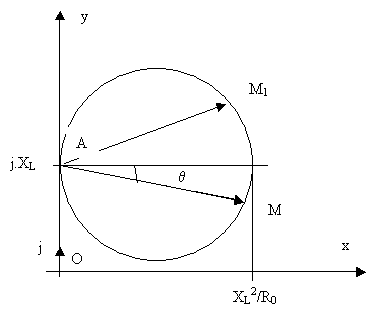
aussi écrire 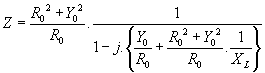
Si on pose![]() , la formule se simplifie en
, la formule se simplifie en ![]()
ce qui correspond à l’équation du cercle de diamètre![]() tangent en O à Oy.
tangent en O à Oy.
Le point M, image de![]() , se déplace donc sur ce cercle (plus précisément, quand XL
varie de 0 (court-circuit) à
, se déplace donc sur ce cercle (plus précisément, quand XL
varie de 0 (court-circuit) à ![]() (self débranchée), le
point M se déplace de O à M0 en tournant dans le sens des aiguilles
d’une montre).
(self débranchée), le
point M se déplace de O à M0 en tournant dans le sens des aiguilles
d’une montre).
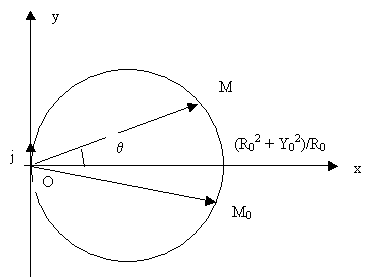
Troisième exemple : représentation graphique d’un
circuit de couplage en G
circuit en gamma
Supposons qu’on dispose d’une impédance comportant une
partie résistive![]() et une partie réactive
et une partie réactive ![]() (par exemple une
antenne non résonante). L’image de
(par exemple une
antenne non résonante). L’image de ![]() dans le plan complexe
est le point M0 . le cadre de la construction d’un circuit d’accord,
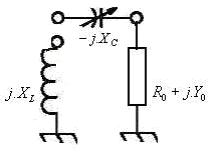
on installe un circuit en Gamma comportant :
dans le plan complexe
est le point M0 . le cadre de la construction d’un circuit d’accord,
on installe un circuit en Gamma comportant :
- en série avec ![]() , un condensateur variable d’impédance
, un condensateur variable d’impédance![]()
- en parallèle sur l’ensemble, une self d’impédance fixe ![]() [1].
[1].
En outre, M1 est l’image de l’impédance Z1 correspondant au
cas où ![]() .
.
La question est de savoir comment varie l’impédance
résultante![]() en fonction des variations du condensateur. Plus précisément,
la question est de savoir comment se déplace dans le plan complexe le point M,
correspondant à
en fonction des variations du condensateur. Plus précisément,
la question est de savoir comment se déplace dans le plan complexe le point M,
correspondant à ![]() . Calculons
. Calculons![]() par les formules habituelles :
par les formules habituelles :
![]() qu’on peut
aussi écrire
qu’on peut
aussi écrire 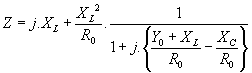
Si on pose ![]() , la formule se simplifie en
, la formule se simplifie en ![]() , ce qui correspond à l’équation du cercle de diamètre
, ce qui correspond à l’équation du cercle de diamètre ![]() tangent à Oy en A,
d’ordonnée
tangent à Oy en A,
d’ordonnée ![]() .
.
Le point M, image de![]() , se déplace donc sur ce cercle (plus précisément, quand
, se déplace donc sur ce cercle (plus précisément, quand ![]() décroît de
décroît de ![]() (circuit coupé) à 0 (court-circuit), M se déplace de A à M1
en tournant dans le sens inverse des aiguilles d’une montre).
(circuit coupé) à 0 (court-circuit), M se déplace de A à M1
en tournant dans le sens inverse des aiguilles d’une montre).