ELECTROMAGNETISME ET NOMBRES COMPLEXES, SECONDE PARTIE
(cette seconde partie est consacrée aux vecteurs et aux champs vectoriels)
Dans la première partie, nous avons vu dans quelles conditions on pouvait associer à des grandeurs scalaires réelles, telles que tensions et intensités, des grandeurs complexes, permettant de simplifier les calculs en éliminant formellement « la variable temps », et donc en ramenant des « calculs en courant alternatif » à des « calculs en courant continu ».
Dans cette seconde partie, nous allons examiner comment transposer les mêmes méthodes aux grandeurs vectorielles. D’un point de vue théorique, la transposition est simple puisqu’un vecteur n’est en fait qu’un ensemble de grandeurs scalaires (ses composantes). Nous ne reviendront donc pas sur la théorie, préférant traiter des principaux exemples rencontrés.
Premier exemple : la polarisation d’un champ
vectoriel sinusoïdal.
Soit, par exemple, une partie de l’espace habituel à 3
dimensions (x, y, z) dans le quel règne un champ électrique sinusoïdal réel 
dont les trois composantes s’écrivent :
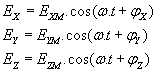
formules dans lesquelles toutes les grandeurs sont réelles,
étant en outre
positifs.
A ce vecteur réel 
, on associe un vecteur complexe 
de composantes :
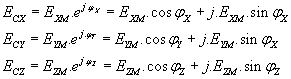
formules dans lesquelles les 3
grandeurs 
sont complexes.
On peut aussi dire que le
vecteur complexe 
est décomposable en deux vecteurs réels suivant : 
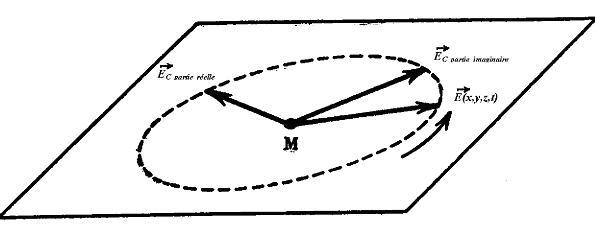
étant le vecteur réel
de composantes 
et
étant le vecteur réel
de composantes 
On passera bien sûr de 
à 
par la
relation :
ce qui conduit
à :
Cette relation est très
importante car elle signifie que le vecteur 
tourne, à la pulsation w,
dans le plan défini par les deux vecteurs 
où son extrémité décrit une ellipse[1].
On dit qu’un tel champ est polarisé elliptiquement.
Second exemple : le champ rayonné à grande distance
par une antenne.
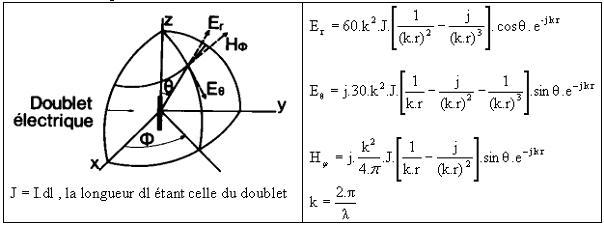
Le champ rayonné par un doublet
électrique de moment J est donné, dans un repère de coordonnées polaires par
les 3 vecteurs complexes 
, 
, 
, les trois vecteurs 
, 
, 
étant les vecteurs
unitaires.
Si nous ne nous intéressons qu’au champ à grande distance, seuls subsistent les termes en (1/r), et donc les seuls vecteurs complexes :
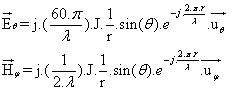
Cette écriture très synthétique
permet de calculer les champs réels instantanés par la méthode que nous avons
vue précédemment (multiplication par 
, puis prise de la seule partie réelle), ce qui donne les
vecteurs réels suivants :
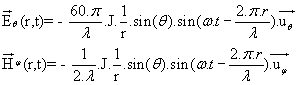
On peut définir un produit scalaire et un produit vectoriel des vecteurs complexes. Par exemple :
- le produit scalaire 
qui est égal au carré du module du vecteur réel
- le produit vectoriel 
qui correspond au
vecteur de Poynting ; dans ce cas, la partie réelle du produit vectoriel
sera interprétable comme représentative de la puissance active et la partie
imaginaire comme représentative de l’ampleur des échanges réactifs.
Troisième exemple : la résolution des équations de
Maxwell.
L’utilisation des vecteurs complexes simplifie beaucoup la résolution des équations de Maxwell, car elle permet de s’affranchir formellement de » la variable temps ». Prenons un l’exemple d’un milieu diélectrique parfait (cas du vide). Dans ce qui suit, nous passerons successivement des vecteurs réels aux vecteurs complexes associés pour revenir enfin aux vecteurs réels, sans toutefois modifier les indices afin de rendre le texte plus lisible.
Dans des milieux homogènes, isotropes et non aimantés, les équations de Maxwell s’écrivent avec les vecteurs réels :
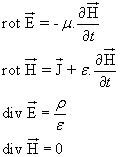
Transposons aux vecteurs
complexes en nous souvenant que la dérivation par rapport au temps est une
opération linéaire qui revient à une multiplication par le facteur 
, et plaçons nous dans le cas du vide (sans charges ni
courants de conduction). En effectuant les calculs, les équations de Maxwell
prennent alors la forme remarquable suivante :
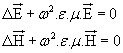
formules dans lesquelles 
est le laplacien,
(par définition,le laplacien 
du vecteur
, en coordonnées rectangulaires, a pour composantes 
).
Si, maintenant, on revient aux vecteurs réels, on obtient :
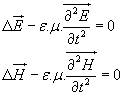
Et on reconnaît là les
équations classiques d’ondes se propageant à la vitesse 
(c étant la vitesse de la lumière).
, c’est-à-dire que les 3 composantes du champ soient en
phase.