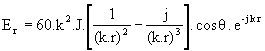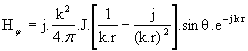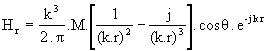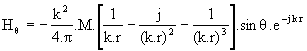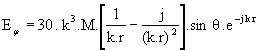ANTENNES DE PETITE TAILLE (rappel de quelques formules)
Une antenne dont la taille est petite par
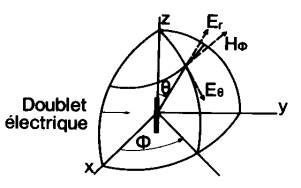
rapport à la longueur d’onde peut se ramener à un doublet, soit électrique,
soit magnétique. Un tel doublet, quand on y fait circuler un courant I,
rayonne, à une distance r, un champ électromagnétique, qu’on en soit près ou
loin, dont les composantes sont les suivantes (nota : les grandeurs
sont exprimées en unités M.K.S.A. et j est le nombre complexe de module 1 et
d’argument p/2) :
Doublet électrique de moment J
|
|
|
, la longueur dl étant celle du doublet
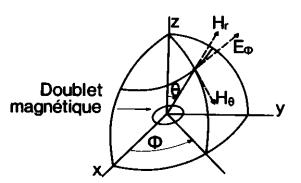
Doublet magnétique de moment M
|
|
|
, le diamètre d étant celui de la boucle
Que peut-on en déduire à propos des composantes du champ électromagnétique ?
Tout près de l’antenne, ce sont les termes en 1/(k.r)3 qui sont prépondérants : ils correspondent aux composantes principales du champ électrostatique et du champ magnétostatique.
Un peu plus loin, les termes en 1/(k.r)2 prennent de l’importance. Ils correspondent à l’induction et sont en particulier à l’origine de Hf pour le doublet électrique et de Ef pour le doublet magnétique.
Enfin, à très grande distance, les termes en 1/(k.r) sont les seuls à avoir de l’importance. Ils correspondent aux formules habituelles du champ rayonné à grande distance (on voit en particulier que le champ n’a plus de composantes radiales Hr et Er).
Que peut-on en déduire en matière énergétique ?
On sait que la puissance surfacique transportée par un champ électromagnétique est mesurée localement par le vecteur de Poynting (les lettres en caractères gras étant des vecteurs) :
P = ½.E ^ H*
c’est-à-dire par le demi-produit vectoriel du vecteur E par le vecteur H* (vecteur complexe conjugué du vecteur H).
Ce vecteur de Poynting a donc une partie réelle et une partie imaginaire, la première correspondant à de la puissance active, la seconde à de la puissance réactive. En faisant le calcul dans le plan (Ox, Oy) par exemple, on trouve, puisque alors q = p/2 :
- dans le cas du doublet électrique, un vecteur radial de module :
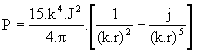formule dans laquelle
P est en Watt/m2
- dans le cas du doublet magnétique, un vecteur radial de module :
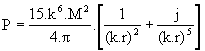formule dans laquelle
P est en Watt/m2
Les puissances s’expriment donc par des formules comparables dont on peut dire que :
- la puissance est proportionnelle au carré de l’intensité dans l’antenne
-
aucune tension, en particulier celle aux bornes de
l’antenne, n’intervient
- la puissance a une partie active et une partie réactive
- la partie active est prépondérante loin de l’antenne (puissance rayonnée)
- la partie réactive est confinée près de l’antenne (puissance non rayonnée)
- cette puissance réactive est capacitive dans le cas du doublet électrique
- cette puissance réactive est selfique dans le cas du doublet magnétique
A grande distance, en intégrant le flux du vecteur de Poynting sur la surface de la sphère de rayon r, on trouve bien sûr la puissance totale rayonnée ; en écrivant que cette puissance totale est égale à la moitié[1] du produit de la résistance de rayonnement Ra de l’antenne par le carré de l’intensité dans l’antenne I, on en déduit la valeur de Ra qui est donc :
- dans le cas du doublet électrique :
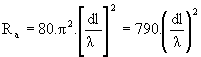, formule dans
laquelle Ra est en W
- dans le cas du doublet magnétique :
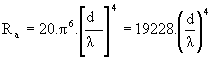, formule dans
laquelle Ra est en W
On retrouve le fait bien connu que des antennes de petite taille ont des résistances de rayonnement très faibles ; par exemple, si on considère un doublet électrique de 1m de long et un doublet magnétique de 1m de diamètre pour la bande des 20m, on trouve :
- dans le cas du doublet électrique : Ra = 2 Ohms environ
- dans le cas du doublet magnétique : Ra = 0,12 Ohms environ